次梯度算法

本文内容包括：次梯度，次微分，次梯度算法

次梯度（Subgradients）

凸函数$f：\mathbb{R}^n \rightarrow \mathbb{R}$的次梯度：存在任意值$g in \mathbb{R}^n$使得： $$f(y) \geq f(x) + g^T(y - x), \forall y$$ 凸函数在不可微时，次梯度可以看做是梯度的一种泛化。除了一些病态条件，凸函数的次梯度总是存在的。对于非凸函数而言，即使上述定义满足，次梯度也可能不存在。 $$f\ differentiable\ at\ x \Rightarrow g = \nabla f(x)[唯一的]$$

次微分（Subdifferentials）

次微分$\partial f(x)$是凸函数f在x点处的次梯度的集合： $$\partial f(x) = \{g \in \mathbb{R}^n: g\ is\ a\ subgradient\ of\ f\ at\ x\ \}$$ 次微分具有如下的性质：

• $\partial f(x)$是封闭的凸集；
• $\partial f(x)$是非空的（如果是非凸函数，则可以为空）；
• 如果f在x处是可微的，则$\partial = \{ \nabla f(x)\}$；
• 如果$\partial f(x) = \{g\}$,那么f在x是可微的，$\nabla f(x) = g$。

次梯度性质

对于一个凸集$C \in \mathbb{R}^n$，它的指示函数(Indicator function)$I_C: \mathbb{R}^n \rightarrow \mathbb{R}$: $$\begin{equation} I_C(x)=I\{ x \in C \}= \begin{cases} 0 \quad & if \, x \in C\\ \infty \quad & if \, x \notin C \end{cases} \end{equation}$$

定理:对于$x \in C,\ \partial I_C(x) = \cal{N}_C(x)$，其中$\cal{N}_C(x)$是C在x点的normal cone:$\cal{N}_C(x)=\{g \in \mathbb{R}^n:g^Tx \geq g^Ty\ \forall y \in C\}$

证明：

• 对于$y \in C$，由于normal cone的性质，$g^Tx \geq g^Ty$，则$0 \geq g^T(y-x)$，又因为$I_C(y) = 0$，因此$I_C(y) \geq g^T(y-x)$
• 对于$y \notin C$，$I_C(y) = \infty \gt g^T(y - x)$,(因为$g^T(y - x)$是有限的)，不满normal cone的定义。

凸函数的次微分具有以下的计算特性：

• Scaling: 在$a \gt 0$时, $\partial (af) = a \cdot \partial f$。如果$a \lt 0$，假设f 是凸函数，那么af 是凹函数，这个等式就不再成立。
• Addition: $\partial (f_1 + f_2) = \partial f_1 + \partial f_2$
• Affine composition: 如果$g(x) = f(Ax+b)$,那么$\partial g(x) = A^T \partial f(Ax+b)$。
• Finite pointwise maximum: 如果$f(x) = \max_{i=1,\cdots,m} f_i(x)$，则 $$\partial f(x) = conv \left(\bigcup_{i:f_i(x)=f(x)}\partial f_i(x)\right)$$ 即$\partial f(x)$是所有有效函数（达到最大值的函数）的次微分集合的凸包，意味着函数f(x)在点x的次微分等于能够取得最大值的函数在该点处的微分。
• General pointwise maximum: 如果$f(x) = \max_{s\in S} f_s(x)$，则 $$\partial f(x) \supseteq cl \left\{ conv \left( \bigcup_{s:f_s(x)=f(x)} \partial f_s(x)\right) \right\}$$
• Norms:使$p,q \gt 0,\ \frac{1}{p} + \frac{1}{q} = 1$。考虑有$f(x) = \left\|x\right\|_p$，其中$\left\|x\right\|_p$被定义为：$\left\|x\right\|_p = \max_{\left\|z\right\|_1 \leq 1} z^Tx$，那么$\partial f(x) = argmax_{\left\|z\right\|_1 \leq 1} z^Tx$。

为什么要用次梯度

当目标函数光滑可微的时候，我们选择使用梯度下降算法，但事实上，并不是所有的目标函数都是光滑，或者处处可微的。如果能够计算次梯度，那么几乎能最小化任何凸函数（可能会很慢，但是是可能的）。

次梯度的优化条件(subgradient optimality condition):对于任意的函数f(不管是否是凸函数)，如果$x^*$是最优解当且仅当0属于f在$x^*$的次梯度的集合： $$f(x^*) = \min_x f(x) \Leftrightarrow 0 \in \partial f(x^*)$$ 证明如下： $$f(x^*) = min_x f(x) \Leftrightarrow f(y) \geq f(x^*) \forall y \Leftrightarrow f(y) \geq f(x^*) + 0^T(y-x^*)\forall y \Leftrightarrow 0 \in \partial f(x^*)$$

如果f是凸函数且是可微的，那么，次梯度优化条件和凸函数的一阶最优性相同。

次梯度算法(Subgradient Method)

与梯度下降算法相似，将梯度替换成次梯度就是次梯度算法. $$x^(k) = x^{(k-1)} -t_kg^{(k-1)},\ k=1,2,3,\cdots$$ 其中$g^{k-1} \in \partial f(x^{(k-1)})$，是在$x^{k-1}$处的次梯度。这个算法不一定是下降的(不一定单调)。

步长选择

• 固定步长：对于所有步长，$t_k = t$。

• 逐渐变小的步长：选择满足如下条件的步长： $$\sum_{k=1}^\infty t_k^2 \lt \infty,\ \sum_{k=1}^\infty t_k = \infty$$

收敛性分析

在前面提到，算法并不是一定是下降的，那么为什么它一定能收敛呢？

如果函数是Lipschitz连续的,$G \gt 0$，即对于所有x,y,$f(x) - f(y) \le G\left\|x-y\right\|_2$。

定理：对于一个固定步长t，次梯度算法满足： $$\lim_{k \rightarrow \infty} f(x_{best}^{(k)}) \le f^* + G^2t/2$$ 对于一个逐渐变小的步长，次梯度算法满足： $$\lim_{k \rightarrow \infty} f(x_{best}^{(k)}) = f^*$$

/ TODO:证明以后来填坑 /

收敛率

次梯度算法的收敛率为$O(1/\epsilon^2)$,与梯度下降算法的收敛率$O(1/\epsilon)$相比，慢了很多。

随机次梯度算法（stochastic subgradient method）

与梯度下降算法的设定相同，考虑凸函数： $$\min_x \sum_{i=1}^m f_i(x)$$

随机次梯度算法迭代： $$x^{(k)} = x^{(k-1)} - t_k\cdot g_{ik}^{(k-1)},\ k=1,2,3,\cdots$$

其中$i_k \in \{1, \cdots, m\}$是在第k次迭代的选择的索引，通过随机或者循环的规则选择，且$g_i^{(k-1)} \in \partial f_i(x^{(k-1)})$。当每一个$f_i$是可微的，这个算法就变成了随机梯度下降算法。

同样随机次梯度算法是可以证明其收敛性和收敛率的。

例子：逻辑回归

给定$(x_i, y_i) \in \mathbb{R}^p \times \{0,1\}$,对于$i = 1, \cdots, n$,逻辑回归的损失函数为： $$f(\beta) = \sum_{i=1}^n \left( -y_i x_i^T \beta + \log(1+ exp(x_i^T \beta)\right)$$

这是一个光滑的凸函数： $$\nabla f(\beta) = \sum_{i=1}^n \left( y_i - p_i(\beta)\right) x_i$$

其中$p_i(\beta) = exp(x_i^T\beta)/(1+ exp(x_i^T \beta)),\ i = 1, \cdots, n$

正则化

正则化的逻辑回归的损失函数为： $$\min \limits_{\beta \in \mathbb{R}^p} f(\beta) + \lambda \cdot P(\beta)$$

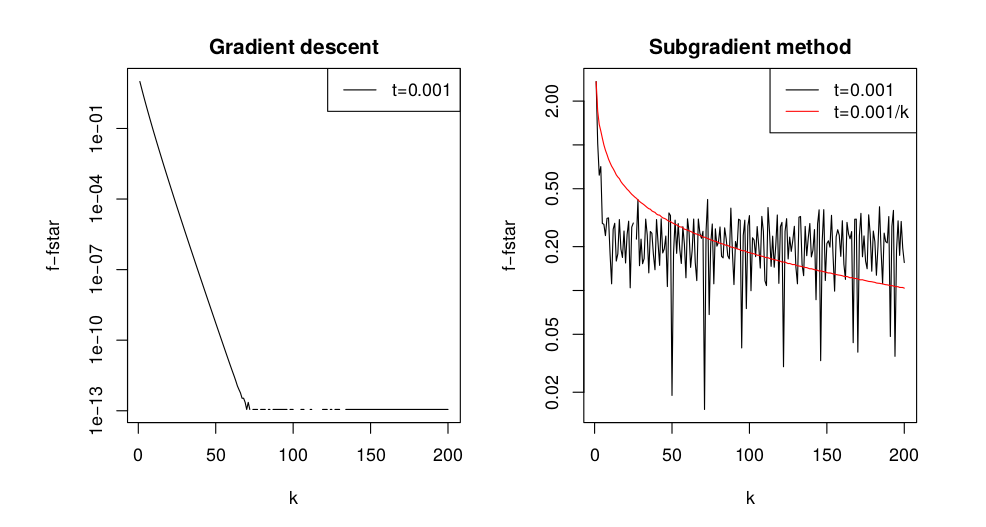
如果$P(\beta) = \left\| \beta\right\|_2^2$，我们称之为岭回归（ridge penalty）；如果$P(\beta) = \left\|\beta\right\|_1$,我们称之为lasso回归（lasso penalty）,对于岭回归，我们可以采用梯度下降算法求解；而对于Lasso问题就需要选择次梯度算法来求解了。下图数据样本n=1000, p=20,左图用岭回归，梯度下降算法，右图用lasso回归，用次梯度算法：

随机梯度下降

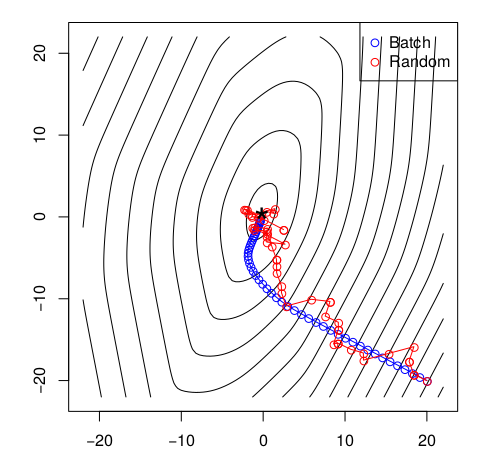
利用SGD算法来求解逻辑回归问题，随机梯度下降与batch梯度下降：

• batch梯度下降时间复杂度：$O(np)$

• stochastic梯度下降时间复杂度：$O(p)$

所以利用随机下降的方法在处理很大批量的数据的时候速度更快，而且前期的表现要好一点，但是后期在最优值处会更加震荡。一张经典的图片可以说明这一点：