梯度下降

本文内容包括:梯度下降算法算法内容和收敛性分析，算法步长选择，梯度提升与随机梯度下降。

梯度下降算法

梯度下降算法是在机器学习和深度学习中应用得十分广泛的算法，了解方向导数，方向余弦，偏导数等数学概念可能会有利于学习这个算法。

$f(x)$是凸函数且在$dom(f)=R^n$上是可微的。将最优的目标函数表示为$f^* = min_x f(x)$，解表示为$x^*$，考虑一个无约束的光滑凸函数优化问题： $$\min_x f(x)$$

梯度下降（Gradient descent）：选择初始点$x^{(0)} \in \mathbb{R}^n$，重复： $$x^{(k)} = x^{(k-1)} - t_k \cdot {\nabla f(x^{(k-1)})}, k = 1,2,3,\cdots$$ 直至在某个点停止。

如何理解梯度下降算法

简单的说，可以将梯度下降算法看做是持续重复地下山，负梯度的方向是降低优化目标函数的方向，那么x沿着负梯度的方向移动一定距离，那么相应的目标函数值就会减少一些，对于凸优化问题来说，不论我们的出发点在哪里，我们总会在最优解附近的某一个点停下来；而对于非凸优化问题，对于不同的出发点，我们可能到达不同的局部最优解。

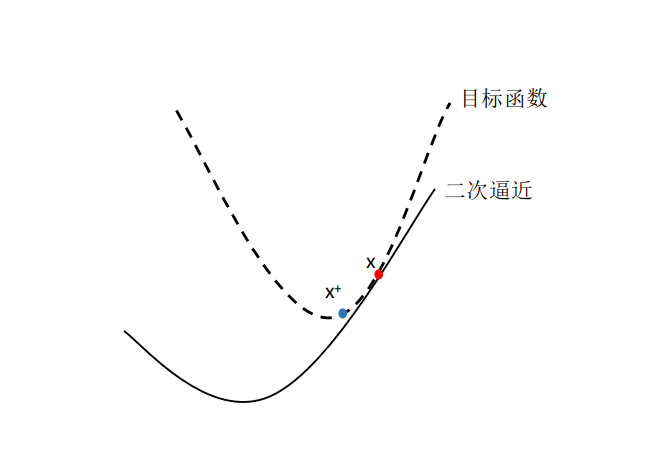
更进一步地，我们可以将梯度下降算法解释为一个二次近似(Quadratic approximation)。假设我们在点x,对f(y)做二次泰勒展开： $$f(y) \approx f(x) + \nabla f(x)^T\cdot (y-x) + \frac{1}{2}\nabla^2f(x)\left\|y-x\right\|^2_2$$

将Hessian$\nabla^2 f(x)$替换为$\frac{1}{t}I$，那么$f(x) + \nabla f(x)^T(y-x)$为f的线性逼近，而$\frac{1}{2f}\left\|y-x\right\|^2_2$，权重为$\frac{1}{2t}$的一个惩罚项，当t越小时，惩罚项却会越大，我们就离开当前x，需要花掉更大的代价(所以在选取步长t时，需要一定的技巧)。这两项，共同构成了f(y)的二次逼近。

梯度下降实际上是在每一步最小化这个二次逼近。 $$\begin{align} min_y f(y) &= min_y \left\{ f(x) + \nabla f(x)\cdot (y-x) + \frac{1}{2t}\left\|y - x\right\|_2^2 \right\} \\ &= min_y \left\{ \nabla f(x)\cdot y + \frac{1}{2t}\left\|y - x\right\|_2^2 \right\} & \text{去除与y无关的项}\\ &= min_y \left\{ 2t \nabla f(x) \cdot y + \left\|y - x\right\|_2^2 \right\} & \text{乘以2t}\\ &= min_y \left\{ 2t \nabla f(x) \cdot y + \left\|y\right\|_2^2 - 2 x\cdot y + \left\|x\right\|^2_2 \right\} & \text{展开}\\ &= min_y \left\{ \left\|y - (x - t\nabla f(x))\right\| \right\} & \text{化简，忽略无关项} \end{align}$$ 为了最小化这个二次逼近，选取$y = x^+$： $$x^+ = x - t\nabla f(x)$$

步长选择

固定步长

最简单的方法是找到一个步长，在所有的迭代过程中，固定步长。但是这样做，是需要一定的技巧与经验的，因为太小的步长会导致迭代过慢，相反，太大的步长可能会导致算法无法收敛。

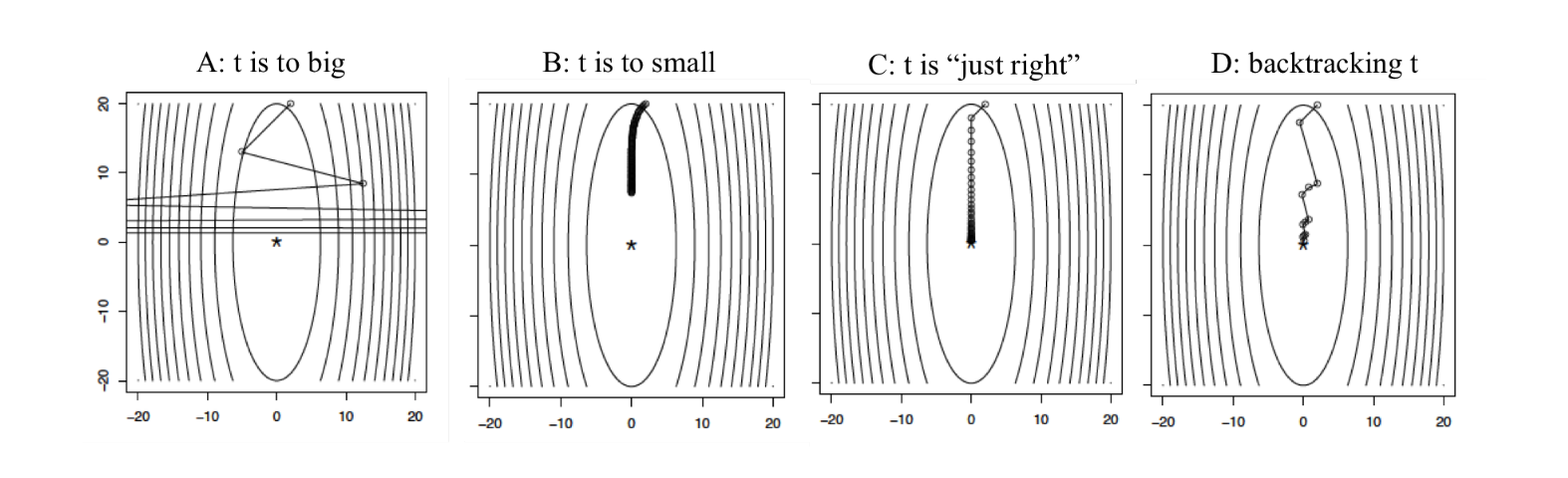
回溯线搜索(Backtracking line search)

通过动态的选择步长是可以的，Backtracking line search就是其中的一种方法，其过程如下：

• 首先固定参数：$0 \le \beta \le 1,\ 0 \le \alpha \le \frac{1}{2}$
• 在迭代的每一步，以$t=t_{init}$开始，当： $$f(x-t\nabla f(x)) \ge f(x) - \alpha t \left\| \nabla f(x) \right\|_2^2$$ 时，缩小$t = \beta t$。否则，进行梯度下降更新： $$x^+ = x -t \nabla f(x)$$

这样做不仅简单，而且在实际应用中表现得很好，进一步简化可以使$\alpha = 1/2$

Exact line search

也可以选择能够沿着扶梯度方向降低的最优步长，被称为exact line search： $$t = \underset{s \geq 0}{\operatorname{argmin}} f(x - s\nabla f(x))$$ 这样做几乎不可能选出合适的步长，因为它消耗的资源比前一种方法更多，并不值得。

收敛性分析

Lipschitz continuous:假设f是可微的凸函数，在$dom(f) = \mathbb{R}^n$，对于任意x,y: $$\left\| \nabla f(x) - \nabla f(y)\right\|_2 \leq L\left\|x -y \right\|_2$$ 即$\nabla f$是Lipschitz连续的，$L \ge 0$。(在证明凸优化算法的收敛性时，这是一个很有用的定理)

假设下面的所有的f都满足上述性质。

定理：对于梯度下降，固定的步长$t \leq \frac{1}{L}$满足： $$f(x^{(k)}) - f^* \leq \frac{\left\|x^{(0)} - x^*\right\|_2^2}{2tk}$$ 我们称梯度下降的收敛率为$O(1/k)$，即为了使$f(x^{(k)}) - f^* \leq \epsilon$，需要$O(1/\epsilon)$次迭代。

/TODO:具体证明，以后来填坑/

特殊情况下的收敛性

backtracking

定理：对于步长通过backtracking line search获得的，梯度下降满足： $$f(x^{(k)}) - f^* \leq \frac{\left\|x^{(0)} - x^*\right\|_2^2}{2t_{min}k},\ 其中t_{min} = \min \{1, \beta/L\}$$

强凸函数的收敛性

具有强凸性质的函数，在满足Lipschitz连续假设的情况下： 定理：对于梯度下降，固定的步长$t \leq \frac{2}{m+L}$，或者通过backtracking line search获得步长，满足： $$f(x^{(k)}) - f^* \leq c^k\frac{L}{2}{\left\|x^{(0)} - x^*\right\|_2^2}，\ 其中0 < c < 1$$ 即强凸函数的收敛率为$O(c^k)$,为指数级的，即为了使$f(x^{(k)}) - f^* \leq \epsilon$，需要$O(\log (1/\epsilon))$次迭代。

实践技巧

停机准则：当$\left\|\nabla f(x)\right\|_2$足够小时停止迭代。

• 在最优解$x^*$处$\nabla f(x^*) = 0$
• 如果f是强凸函数，参数为m，有： $$\left\|\nabla f(x)\right\| \leq \sqrt{2m\epsilon} \Rightarrow f(x) - f^* \leq \epsilon$$

优点：

• 简单，每次迭代代价相对较小
• 对于有良好条件的强凸问题速度很快

缺点：

• 一般情况下收敛速度并不快
• 不能解决不可微的函数

扩展

梯度提升(Gradient Boosting)

梯度提升是梯度下降与树相结合的一种方法。假设观测值$y=(y_1, \cdots, y_n) \in R^n$， 预测器$x_i \in R^p, i=1,\cdots,n$。我们想基于我们的预测器构建一个非线性的模型。

我们定义树的加权和如下： $$u_i = \sum_{j=1}^m \beta_j \cdot T_j(x_i),\ i=1,\cdots, n$$

每一个树$T_j$将一个预测器$x_i$作为输出并输出一个预测值。在这种设定下，选择一个损失函数L，例如在y连续时，我们可以选择$L(y_i, u_i)=(y_i -u_i)^2$，于是，问题转变为： $$\min \limits_{\beta} \sum_{i=1}^n L\left( y_i, \sum_{j=1}^M \beta_j \cdot T_j(x_i) \right)$$

将这个优化问题想象成$min_u f(u)$，这个算法的执行情况如下：

从一个初始的模型（一个简单的树$u^{(0)} = T_0$）开始，重复：

1. 计算上一次预测$u^{k-1}$的负梯度d， $$d_i = - \left[ \frac{\partial L(y_i, u_i)}{\partial u_i}\right]\bigg|_{u_i=u_i^{(k-1)}}, i=1,\cdots,n$$

2. 寻找一个树接近d，也就是说： $$\min \limits_{trees T} \sum_{i = 1}^n (d_i - T(x_i))^2$$

3. 计算步长$\alpha_k$,更新我们的预测值： $$u^{(k)} = u^{(k-1)} + \alpha_k \cdot T_k$$

随机梯度下降(Stochastic Gradient Descent)

考虑最小化函数的加和： $$\min \limits_{x} \sum_{i=1}^m f_i(x)$$

梯度下降迭代计算： $$x^{(k)} = x^{(k-1)} - t_k \cdot \sum_{i=1}^m \nabla f_i(x^{(k-1)}), k=1,2,3,\cdots$$

随机梯度下降（SGD）迭代计算： $$x^{(k)} = x^{(k-1)} - t_k \cdot \nabla f_{i_k}(x^{(k-1)}), k=1,2,3,\cdots$$

其中$i_k \in \{1, \cdots, m\}$是在第k次迭代的时候选择的指数。

有两种规则可以选择$i_k$:

• 循环的方法：选择$i_k =1,2,3,\cdots,m,1,2,3,\cdots,m$

• 随机的选择：通过随机的方式选择$i_k \in \{1,\cdots, m\}$，在实际应用中选择这种方式更多。

可以证明SGD算法在$\nabla f_i(x)$不随x剧烈变化时是收敛的。