优化基础

本文内容包括：凸优化的术语，凸解集，支持向量机的凸优化问题，局部优化，变量的变换与改变，消除等式约束，引入松弛变量等凸优化问题的转化，把PCA写成凸优化问题。

术语

我们定义一个凸优化问题如下: $$\begin{split} \min \limits_{x \in D} \quad & f(x)\\ subject\ to\ \quad & g_i(x) \leq 0, i = 1, \cdots,m；\\ & Ax=b\\ \end{split}$$

其中目标函数，${\mit f}$,和不等的约束函数，${\mit g_i}$，都是凸函数，同样，等式约束是线性的。以及，定义域是$D = dom(f) \cap \bigcap_{i=1}^m dom(g_i)$。

凸优化涉及到的术语如下：

• ${\mit f}$:目标函数(objective/criterion function)
• ${\mit g}$:约束条件(inequality constaraint functions)
• ${\mit x}$可行解(feasible point):任何满足优化问题的约束条件的${\mit x}$
• ${\mit f^*}$最优值(optimal value):所有可行解中,目标函数的最小值
• ${\mit x^*}$最优解(optimal/solution)：$if\ x^* \in x\ s.t.\ f(x^*)=f^*$
• $\epsilon-suboptimal$解：满足$f(x) \leq f^* + \epsilon$ 的可行解

如果${\mit x}$是可行解且$g_i(x) = 0$，则$g_i$在${\mit x}$ 处是活跃的(active)，而如果$g_i(x) \le = 0$，则$g_i$在${\mit x}$ 处是待用的(inactive)。

任何凸函数的最小化都可以转换成一个凹函数的最大化，反之依然。这是因为，在约束条件下最小化$f(x)$，等于在相同的约束条件下最大化$- f(x)$，他们具有相同的解。

凸解集

如果$X_{opt}$是一个凸优化问题的所有最优解的集合，它可以被表达为： $$\begin{split} X_{opt}= \quad argmin \quad & f(x)\\ subject\ to\ \quad & g_i(x) \leq 0, i = 1, \cdots,m\\ & Ax=b\\ \end{split}$$

那么这样的一个最优解集是否是凸集呢？可以通过考虑两个最优解x,y来验证其凸性质。对于$0 \leq t \leq 1,\ tx+(1-y)y \in D$，由于x,y满足不等和相等约束： $$f(tx+(1-t)y) \leq tf(x) + (1-t)f(y) = tf^* + (1-t)f^* = f^*$$ 所以$tx + (1-t)y$也是一个最优解，$X_{opt}$是一个凸集。但是$X_{opt}$是凸集，不意味它是唯一的。也就是说，即使一个局部最优解就是全局最小，一个凸优化问题的解仍然有很多。这些优化问题可能有零个，一个和无数多个解。如果凸函数具有严格凸性质，那么它只有唯一的解。

例子：Lasso

Lasso是一个在机器学习和统计学中十分常见的问题，它是一个回归问题。

给定$y \in R^n$，且$x \in R^{n*p}$，一个Lasso问题可以公式化为： $$\begin{split} \min_{\beta} \ & \left\|y -X\beta\right\|_2^2\\ subject\ to \ & \left\|\beta\right\|_1 \leq s\\ \end{split}$$

Lasso 是一个凸优化问题因为目标函数是一个最小二乘损失的凸函数，而且它的越是一个范数小于一个常数，而它也是凸的。这个问题只有一个不等式约束，$g_i(x) = \left\|\beta\right\|_1 -s$，没有等式约束。可行解集是满足L1-范数球的$\beta \in R^p$。

• $n \geq p$, X 满秩：这样$\nabla^2f(\beta)=2X^TX$，给定X是满秩 $\Rightarrow$ $X^TX$是不可逆的 $\Rightarrow$ $X^TX$是正定的。因此，$\nabla^2f(\beta) \ge 0$，在这种情况下最优解是唯一的因为严格凸函数只有一个最优解。

• $p \ge n$(高维)情况：在这种情况下，$X^TX$是奇异的。$f(\beta)= \beta^TX^TX\beta - 2y^TX\beta + y^Ty$，对于一些$\beta \not= 0 且X\beta = 0$，我们得到$\beta^TX^TX\beta=0$。这意味着$f(\beta)$是线性的。因此，我们得到多个解而且不能保证有唯一解。

如果一个函数f是严格凸函数，这意味着解的唯一性，否则我们不能保证唯一性。

例子：支持向量机

支持向量机是一种解决分类问题的机器学习算法，一般用于解决线性可分的二分类问题，在加入了核函数之后，也可以用于非线性可分的问题。

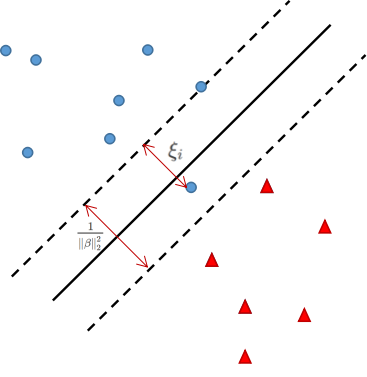
给定标签$y \in \{-1,1\}^n$和特征$X \in R^{n \times p},\ 行向量x_1, \cdots, x_n$,有两个变量($\beta和\xi$)，$\frac{1}{\left\|\beta\right\|_2^2}$是分类的虚线边界的聚义，$\xi_i$为分类错误的代价，代表分错的样本点到正确分类边界的距离，间距$\beta_0$是单维度的参数，C是一个选择的参数，SVM的目标函数是： $$\min_{\beta,\beta_0, \xi} \frac{1}{2}\left\|\beta\right\|_2^2 + C \sum_{i=1}^n \xi_i$$

它的优化约束是： $$\xi_i \geq 0, i=1, \cdots, n$$ $$y_i(x_i^T\beta + \beta_0) \geq 1 - \xi_i, i =1,\cdots,n$$

这个问题是凸优化问题，因为目标函数仅仅是一个二次加一个线性函数（凸函数）,我们可以重写$-\xi_i \leq 0$，是一个仿射函数，同样我们可以重写第二个不等式约束$-y_i(x_i^T\beta + \beta_0) +1 -\xi_i \leq 0$。

这个问题不是严格凸的因为目标函数是$\xi$的一个线性函数。因此，我们不能说它有唯一的最优解。

特殊情况：如果我们固定其他变量，只看$\beta$组分，它决定分割的超平面的位置，那么目标函数就是一个严格凸函数，就有唯一解。

重写约束

针对凸优化问题，在不失概括性的情况下，我们可以将约束封装在集合C中，

根据$x \in C$，其中$C = \{x:g_i(x) \leq 0, i=1,\cdots, m; Ax=b\}, the\ feasible\ set\ $。说$x \in C$也就是说在C中描述的约束都满足。更进一步，我们可以用C的指示函数$I_C$来重写凸优化问题： $$\min_x f(x)+I_C(x)$$ 这个指示函数$I_C$当$x \in C$时，等于0，当$x \notin C$，等于无限。当C为凸集时，只是函数是一个凸函数。利用凸函数的定义，如果$g_i(x)$为凸函数，那么$g_i(x) \leq 0$为凸集。而对于所有的i来说，都有$g_i(x) \leq 0$，是凸集的intersection。因此C是由凸约束构成的凸集： $$C = \cap_{i=1}^m\{x:g_(x) \leq 0\}\cap\{x:Ax=b\}$$

一阶最优性

一阶最优性(first-order optimality)是凸函数的充要条件，这描述同样使用于凸优化问题。 $$\begin{split} \min_x \ & f(x)\\ subject\ to\ & x \in C\\ \end{split}$$ 令f为可微的，那么一个可行点是最优点的充要条件是： $$\nabla f(x)^T(y-x) \geq 0,\ for\ all\ y \in C.$$ x的所有可行的方向与梯度一致。

解释:假设你在一个可行点x，你打算移动到另一个可行点y,如果从x到y的向量与梯度一致，如果对于所有的y,x到他们的梯度都是正的，那么x就是最优解。相当于，你站在山谷的一个点上，你向四周爬都是在向上爬，那么你站的点就是最低点。

特殊情况：$C = R^n$时，就是没有约束的优化(全局)，当尝试最小化一个凸的光滑函数f时，这个最优解必定在梯度为0的地方。

例子：quadratic minimization

考虑最小化： $$f(x) = \frac{1}{2}x^TQx + b^Tx + c，\ where\ Q \geq 0.$$ 它的一阶条件显示最优解满足： $$\nabla f(x)= Qx + b = 0$$ 根据Q的不同有三种可能的最优解的情况：

• 如果$Q \geq 0$如正定的，那么有一个唯一解$x = -Q^{-1}b$
• 如果Q是奇异的，如不可逆，且$b \notin col(Q)$，那么无解
• 如果Q是奇异的，如不可逆，且$b \in col(Q)$，那么有无限多个解，解的形式是$x = Q^+b + z, 其中z \in null(Q),且Q^+是Q的伪逆$

局部优化

通常可以局部优化一个凸优化问题而且保持凸性质。

这基于一个事实，即只要最小化的集合是凸的，我们就可以总是将函数局部最小化到某些变量上。

通常地：$g(x) = \min_{y \in C}f(x,y)$，f在(x,y)上是凸函数，并且C是凸集。

例如，如果我们分解x,$x=(x_1, x_2) \in R^{n_1 + n_2}$： $$\begin{split} \min_{x_1,x_2} \ & f(x1,x2)\\ s.t.\ \ & g_1(x_1) \leq 0\ , g_2(x_2) \leq 0\\ \end{split}$$ 在局部上，我们同样可以： $$\begin{split} \min_{x_1} \ & \tilde{f}(x_1)\\ s.t.\ \ & g_1(x_1) \leq 0,\ where\ \tilde{f}(x_1)=\min\{f(x_1, x_2):g_2(x_2) \leq 0\}\\ \end{split}$$ 如果第一个问题是凸的，那么第二个问题也是凸的。

例子：hinge form of SVMs

可以将前面的SVM改写：

首先重写约束条件为$0 \leq \xi_i，\ 1 - y_i(x_i^T\beta+\beta_0) \leq \xi_i$或者$\xi_i \geq \max\{0, 1-y_i(x_i^T\beta + \beta_0)\}$。这个不等式在优化时通常是大于，只有在最优解的时候为等于。这意味着我们可以最小话$\xi_i$应为我们已经知道了在最优解时的情况：$\xi_i=\max\{0, 1-y_i(x_i^T\beta+\beta_0)\}$。

因此插入最优的$\xi$我们可以重写这个问题： $$\min_{\beta,\beta_0}\frac{1}{2}\left\|\beta\right\|_2^2 + C\sum_{i=1}^n[1-y_i(x_i^T\beta + \beta_0)]_+$$ 其中$a_+ = \max\{0, a\}$被成为hinge function。

变量的变换与改变

• 变换(transforming variables)

如果$h:R \rightarrow R$是单调递增的变换， $$\min_x f(x)\ s.t.\ x \in C \Leftrightarrow \min_x h(f(x))\ s.t.\ x \in C$$ 相似地，不等式和等式约束可以被转换并产生相同的优化问题。我们在统计学上经常遇到这种，比如我们经常用对数似然函数替代似然函数因为log函数是单调递增的。可以利用变换来解决一些隐藏的凸优化问题。

• 改变(changing variables)

如果$\phi:R^n \rightarrow R^m$是一对一的，且它的图像包含了可行解集C. $$\min_x f(x) s.t.\ x \in C \Leftrightarrow \min_y f(\phi(y))\ s.t.\ \phi(y) \in C$$

消除等式约束

如果一个问题可以写成一个标准的凸优化形式： $$\begin{split} \min \limits_{x \in D} \quad & f(x)\\ subject\ to\ \quad & g_i(x) \leq 0, i = 1, \cdots,m；\\ & Ax=b\\ \end{split}$$ 那么，x可以表示为$My+x_0(where\ Ax_0 =b\ and\ col(M) = null(A) )$。这样做可以使我们的重写上述问题为： $$\begin{split} \min \ & f(My +x_0)\\ s.t.\ \ & g_i(My +x_0) \leq 0, i=1,\cdots,m\\ \end{split}$$

引入松弛变量

松弛变量的概念与消除等式约束完全相反，因此凸优化可以写成： $$\begin{split} \min \limits_{x，s} \quad & f(x)\\ subject\ to\ \quad & s_i \geq 0, i = 1, \cdots,m；\\ & g_i(x) + s_i = 0, i =1, \cdots,m;\\ & Ax=b\\ \end{split}$$

这个问题不是凸优化问题除非$g_i$全是仿射的（affine）

放宽非仿射等式约束

给定一个优化问题$\min_xf(x),\ x \in C$，我们可以考虑把C放大，$\tilde{C} \supseteq C$，然后最小化$\min_xf(x),\ x \in \tilde{C}$。这种方法被称为relaxation，新问题的最优解通常小于或者等于原问题的最优解。

一个重要的特殊情况是将所有的凸非仿射等式约束$h_j(x)=0, j=1,\cdots,r$用$h_j(x) \leq 0, j=1,\cdots, m$取代。

例子：最大效用问题

最大效用问题(maximum utility problem)是投资/消费等问题的模型，它可以被公式化为： $$\begin{split} & \max_{x,b} \sum_{t=1}^T\alpha_tu(x_t)\\ s.t.\ \ & b_{t+1} = b_t + f(b_t) -x_t, t=1, \cdots, T\\ & 0 \leq x_t \leq b_t, t=1, \cdots, T\\ \end{split}$$ 其中$b_t$为预算，$x_t$为时间t的消费总数，f是投资返回函数，u为效用函数，它们都是凹的，且是增加的。这个等式约束不是仿射的，但是我们可以将它松弛成一个不等式约束(等号变小于等于)，这个问题就是凸优化问题了。

例子：主成分分析

主成分分析(Principal component analysis)也是一种常见的机器学习算法，它主要用于提取高维数据中的主成分并降维到更地位。降维可以解决维度灾难的问题。

给定$X \in {\cal R}^{n \times p}$，考虑低秩近似问题$min_R \left\|X-R\right\|_F^2$

其中$rank(R)=k$，$\left\|A\right\|_F^2=\sum_{i=1}^n\sum_{j=1}^pA_{ij}^2$为entrywise squared $l_2$ norm。

这也被称为主成分分析问题，在PCA中，$X=UDV^T$是X的奇异值分解，最优解可以表示为 $$R=U_kD_kV_k^T$$ 其中$U_k$和$V_k$是U和V的前k列，$D_k$是D的前k个对角线元素。R相当于是从X的前k个主成分中重建。

这并不是一个凸优化问题，因为$C=\{R:Rank(R)=k\}$不是凸集。

这个问题可以改写成凸优化的形式： $$\min_{Z \in {\cal S^P}}\left\|X-XZ\right\|_F^2\ s.t.\ rank(R)=k \Leftrightarrow \max_{Z \in {\cal S^P}}\ tr(SZ)\ s.t.\ rank(R)=k$$

其中Z是一个投影，$S=X^TX$，因此，约束集是非凸的集合： $$C = \{Z \in {\cal S^P}: \lambda_i(Z) \in \{0,1\},i=1, \cdots, p,\ tr(Z) = k\}$$

其中$\lambda_i(Z)$是Z的n个特征值，对于这样的提法，最优解为$Z=V_kV_k^T$，其中$V_k$为V的前k列。

如果将约束集松弛到${\cal F}=conv(C)$,即它的凸包中。

注意 $$\begin{split} {\cal F_k}\ & =\ \{Z \in {\cal S^P}:\lambda_i(Z) \in [0,1], i = 1,\cdots,p,\ tr(Z) = k \}\\ & =\ \{Z \in {\cal S^P}:0 \leq Z \leq I,\ tr(Z)=k\}\\ \end{split}$$ 这被称为order k的Fantope。

因此，在Fantope上线性最大化： $$\max_{Z \in {\cal F_k}}\ tr(SZ)$$ 是一个凸优化问题，这和非凸的PCA问题是等同的，他们有相同的结果。