凸集与凸函数

本文内容包括: 凸集与凸函数的定义、性质、运算操作和例子，softmax函数是凸函数。

凸集

定义

凸集: $C \in {\cal R}^n$ 是一个凸集如果$x, y \in {\cal C} \Rightarrow tx + (1-t)y \in {\cal C}, 其中 0 \leq t \leq 1.$

换句话说，在集合内任意两个元素连接成的直线上的点也在该集合内，这样的集合叫做凸集。

上图中，左边的集合是凸集，而右边的集合不是。

凸组合： ${\mit x_1,..., x_k \in R^n}$ 的凸组合是一个任意的线性组合 $$\theta_1x_1+...+\theta_kx_k$$ 其中 $\theta_i \geq 0 , i = 1, ..., k,$而且$\sum_{i=1}^k \theta_i = 1$

凸包：集合${\cal C}$的凸包${\cal conv(C)}$,是集合中元素的所有凸组合。一个凸包总是凸的，但是集合${\cal C}$不需要是凸的。

凸集的例子

• 特定的集合（Trivial）: 空集， 点，线
• 范数球(Norm ball): $\{ x: \left\| x\right\| \leq r \}$， 对于给定范数$\left\| \cdot \right\|$, 半径${\cal r}$
• 超平面（Hyperplane）: $\{x:a^Tx=b\},\ for\ given\ a\ ,b.$
• 半空间（Halfspace): $\{x:a^Tx \leq b\}$
• 放射空间（Affine space):$\{x: Ax = b\},\ for\ given\ a\ , b.$
• 多面体（Polyhedron):$\{x: Ax \leq b\}$

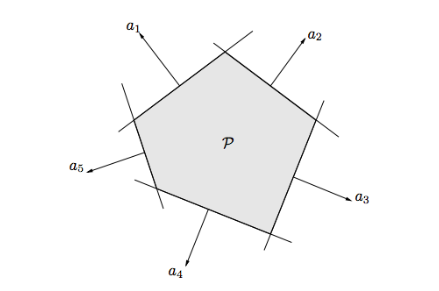
• 单面（simplex)

锥（Cones）

定义

Cone是一个集合${\mit C \subseteq R^n}$满足： $$x \in C \Rightarrow tx \in C\ for\ all\ t \geq 0$$

Convex cone是一个凸的锥，例如： $$x_1, x_2 \in C \Rightarrow t_1x_1 + t_2x_2 \in C\ for\ all\ t_1, t_2 \geq 0$$ 凸锥的实例如下图所示:

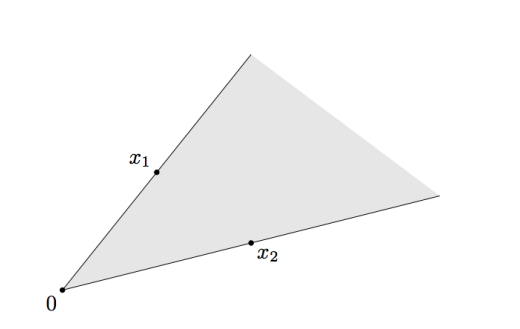
锥组合： ${\mit x_1,..., x_k \in R^n}$ 的凸组合是一个任意的线性组合： $$\theta_1x_1+...+\theta_kx_k$$ 其中 $\theta_i \geq 0 , i = 1, ..., k$。

锥包（Conic hull):是所有锥组合的集合：$\{\sum_i\theta_ix_i: \theta \in R_+^k\}$

凸锥的例子

• Norm cone: $\{(x,t):\left\| x \right\| \leq t\}$,当这个范数是使用的2范数$\left\| \cdot \right\|_2\$的时候，被称为second-order cone.

• Normal cone: 给定集合C与点$x \in C$，可以定义: $${\cal N_C(x)} = \{g: g^Tx \geq g^Ty, for\ all\ y \in C\}$$

满足该定义的点的集合都是Normal cone,其含义是指在normal cone中的点与集合C内的点的内积永远大于集合C内任意点与x的内积。

• Positive semidefinite cone: $S_+^n = \{ X \in S^n: X\geq 0\}$--正半定锥

• Positive semidefinite: 一个矩阵X是正半定的当X的所有特征值都大于等于0 $\Leftrightarrow \ a^TXa \geq 0\ for\ all\ a \in R^n$。

凸集的主要性质

凸集有两个重要的性质，这对于机器学习中的分类问题(如SVM)来说，在理论上起着支撑作用。

1. 分隔超平面理论（Separating hyperplane theorem）:两个不相交的凸集之间存在一个分割超平面。一个正式定义是：如果C、D是非空的凸集，且$C\cap D=\emptyset$，那么存在a,b使得： $$C \subseteq \{x:a^Tx \leq b\}\\ D \subseteq \{x:a^Tx \geq b\}$$ 如下图所示:

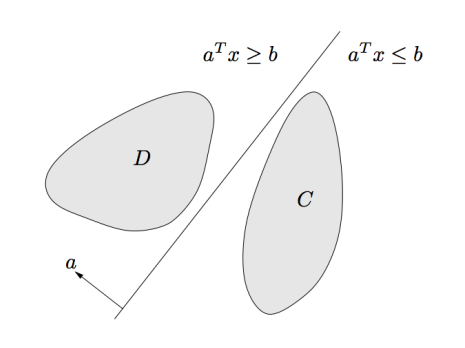
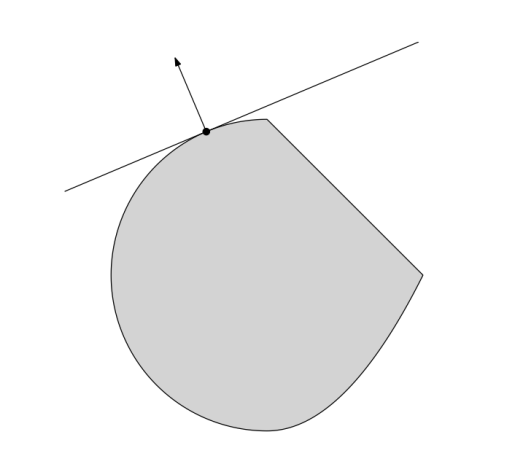
2. 支撑超平面理论（Supporting hyperplane theorem):如果C是一个非空的凸集，而且$x_0 \in {\mit boundary(C)}$，那么存在一个a使得： $$C \subseteq \{x: a^Tx \leq a^Tx_0\}$$

保存凸性质的操作

• 交（intersection):凸集的交集依然是凸集。
• Scaling and translation: 如果C是凸集，那么$aC + b = \{ax + b:x \in C\}$也是凸集，对于任意的a,b。
• Affine images and preimages: 如过$f(x)=Ax+b$和$C$是凸的，那么$f(X) = \{f(x):x\in C\}$ 也是凸集；如果$D$是凸集那么$f^{-1}(D) = \{x:f(x) \in D\}$也是凸集。

凸函数

定义

凸函数: $f : {\cal R^n } \rightarrow {\cal R}$是凸函数如果${\mit dom(f)} \subseteq {\cal R^n } 是凸的,且f(tx + (1-t)y) \leq tf(x) + (1-t)f(y), 其中 0 \leq t \leq 1.$

如图所示，f总是在$（x,f(x)), (y,f(y))$的直线连线的下方。

凹函数与凸函数有着相反的定义，我们可以推出： $$f\ concave \Leftrightarrow -f\ convex$$

凸函数有两个重要的分类（修饰符）：

• 严格凸性质（Strictly convex）: 这意味着$f(tx + (1-t)y) \le tf(x) + (1-t)f(y), for\ 0 \leq t \leq 1$对于$x \not= y\ and\ 0 \le t \le 1.$换句话说，f是凸函数而且曲率比线性函数大。

• 强凸性质（Strongly convex）:有参数$m \ge 0$使得$f - \frac{m}{2}\left\|x\right\|_2^2$是凸函数。也就是，f至少像二次函数一样的凸函数。

$强凸性质 \Rightarrow 严格凸性质 \Rightarrow 凸性质$，例如函数$f(x) =1/x$是严格凸的，但是不是强凸性的。

凸函数的例子

• 单变量函数
  • 指数函数
  • 幂函数 $$\begin{eqnarray} x^a = \begin{cases} convex, &a \geq 1\ or\ a \leq 0\cr concave, &0 \leq a \leq 1\end{cases} \end{eqnarray},在{\cal R_+}上$$
  • 对数函数（$\log x$在${\cal R_{++}}$上是凹的。）
• 仿射函数: $a^Tx+b$既是凹的也是凸的。
• 二次函数: $\frac{1}{2}x^TQx + b^Tx + c$是凸函数如果$Q \geq 0$
• 最小二乘损失：$\left\|y-Ax\right\|_2^2$总是凸函数，因为$A^TA$总是正半定的。
• 范数$\left\|x\right\|$是凸函数（任何范数）
• 指示函数（indicator function):如果C是凸集，那么它的指示函数 $$\begin{eqnarray} I_C(x)=\begin{cases} 0,&x \in C\cr \infty, &x \notin C \end{cases} \end{eqnarray}$$ 也是凸函数。
• 支撑函数（support function）：对于任意集合C(不论是否是凸集)，它的支撑函数$i_C^*(x) = \underset{y \in C}{max}\ x^Ty$是凸函数
• 最大函数$f(x) = max\{x_1, \cdots,x_n\}$是凸函数。

凸函数的主要性质

Epigraph characterization:一个函数是凸函数当且应当其epigraph是凸集，其中epigraph被定义为： $$epi(f) = \{(x,t) \in dom(f) \times R: f(x) \leq t\}$$ 简单的说，epigraph是函数图像上方的点的集合。

Convex sublevel sets:如果f是凸函数，那么它次层集合$\{x \in dom(f): f(x) \leq t\}$也是凸的，对于所有的$t \in {\mit R}$。反之则不成立。

First-order characterization:如果f是可微的，那么f的凸函数当且仅当dom(f)是凸的，且$f(y) \geq f(x) + \nabla f(x)^T(yx)\ for\ all\ x,y \in dom(f)$。也就是说，f必须在它的切线超平面上方。因此，对于一个可微的f, x最小化f当且仅当$\nabla f(x) = 0$。

Second-order characterization:如果f是二次可微的，那么f是凸函数当且dom(f)是凸集。而且它的Hessian矩阵$\nabla^2 f(x) \geq 0\ for\ all\ x\ \in dom(f)$。

Jensens inequality:如果f是凸函数，而且X是f的定义域上的一个随机变量，则$f(E[X]) \geq E[f(X)]$。

保存凸函数性质的操作

• 非负的线性组合

• pointwise maximization：定义一个新的函数f(x)在x的值为有限可数的凸函数在x处的最大值，则f为凸函数，这意味着我们总能以逐点的方式最大化一系列函数。

• partial minimization：如果$g(x, y)$在x, y上是凸函数，而且C是一个凸集，那么在凸集C上的任意变量上局部最小化函数也是凸函数，如$f(x)=min_{y \in C} g(x,y) 和 f(y) = min_{x \in C} g(x,y)$

• 仿射组合：如果f是凸函数，那么$g(x)=f(Ax+b)$也是凸函数。

• General composition:$f(x)=h(g(x))$是凸函数当：外层函数h：$R \rightarrow R$是单调的，且内层函数g:$R^n \rightarrow R$是凹函数或者凸函数。

  • f是凸函数，如果h是凸函数且不单减，g是凸函数
  • f是凸函数，如果h是凸函数且不单增，g是凹函数
  • f是凹函数，如果h是凸函数且不单减，g是凹函数
  • f是凸函数，如果h是凸函数且不单增，g是凹函数

• 向量组合：与general composition相似，不过是逐点的形式。

例子：Softmax函数

Log-sum-exp（LSM）函数是： $$g(x) = \log(\sum_{i=1}^k exp(a_i^Tx + b_i))$$ 对于固定的$a_i和b_i$。

Log-sum-exp是凸函数，是严格单调递增的函数，但是并不是具有严格凸性质的。log-sum-exp可以选出平滑的最大值，利用切线逼近$\log(X+a) \approx \log X +a/X$，如果某一项$x_j$比其他的所有项都大： $$LSE(x) = \log(\sum_i exp\ x_j) \approx \log(exp\ x_j) + (\sum_{i \neq j} exp\ x_i)/exp\ x_j \approx x_j = max_i\ x_i$$

$x = (x_1, \cdots, x_n)$，则偏导数是： $$\frac{\partial}{\partial x_i} LSE(x) = \frac{exp\ x_j}{\sum_j exp\ x_j}$$ 用梯度表示偏导数作为向量，可以得到softmax函数，一个在机器学习中被广为应用的函数。

话说回来，为什么log-sum-exp是凸函数呢？

由于仿射组合会保存凸性质，所有只要证明$f(x) = \log(\sum_{i=1}^k exp(x_i))$是凸函数就可以了。通过f(x)的二阶性质我们可以证明其凸性质: $$\nabla_i f(x) = \frac{e^{x_i}}{\sum_{l=1}^n e^{x_l}}$$

$$\nabla_{ij}^2 f(x) = \frac{e^{x_i}}{\sum_{l=1}^n e^{x_l}}1\{i=j\} - \frac{e^{x_i}e^{x_j}}{(\sum_{l=1}^n e^{x_l})^2}$$ （我也不知道这个二阶导是怎么求的。数学堪忧。。）

重写前一个公式有$\nabla^2 f(x)= diag(z) - zz^T$，其中$z_i = e^{x_i}/(\sum_{l=1}^n e^{x_l})$，这个矩阵是严格对角占优的，所以是正半定的（p.s.d）,根据凸函数的二阶性质，f(x)是凸的。

例子：函数$max\{\log \big (\frac{1}{(a^Tx+b)^7}\big ), \left\|Ax+b\right\|_1^5\}$是凸函数吗？

在这个课程中，还讲了这样一个例子，上述函数是凸函数吗？

答案是是凸函数，它可以通过凸函数的性质与保存凸函数性质的操作得到。